Filtros pasivos
Introducción
Los filtros pasivos son los primeros en su tipo; estas cumplen una función muy importante en la electrónica, la cual es filtrar las señales que no se desean en un proceso. También, en el caso de los sonidos, para separar las señales con frecuencias altas, medias y bajas; con ello se logra una óptima salida sin pérdida de frecuencias. Por lo anterior, en este laboratorio, se estudiará el principio de funcionamiento de este tipo de filtros, con elementos pasivos cómo son las resistencias, bobinas y condensadores.
Objetivos
- Medir la respuesta en frecuencia de los filtros.
- Medir la frecuencia de corte de un filtro pasa altas, pasa bajas, pasa banda y rechaza banda.
Equipos y Materiales
- Osciloscopio
- Generador de funciones
- Multímetro
- Protoboard
- (01) Resistencia 10K 1/4W
- (01) Resistencia 1K 1/4W
- (01) Resistencia 100 Ohm 1/4w
- Cables de conexión
Preparación
Se recomienda tener una lectura previa del capítulo 4 del libro Síntesis de Redes-Impedancias y Filtros que pertenece a José Espi López, Rafael Magdalena Benedito.
Procedimiento
Filtro Pasa bajos
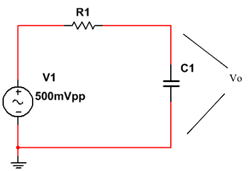
- Escribir, para la configuración de la Figura, las ecuaciones que definen las características siguientes:
fc: frecuencia de corte
Av: Ganancia de tensión
G db: Ganancia en decibeles
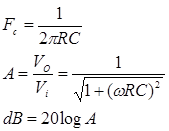
-
Con los datos proporcionados calcular cada una de las características citadas
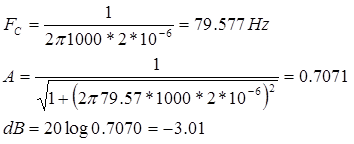
- Montar el circuito. Ajustar el generador de funciones para que proporcione una onda senoidal de 500mV (pico) y frecuencia de 1KHz, y aplicar esta señal a la entrada del circuito. Finalmente, conectar a la entrada 1 del osciloscopio a la entrada del circuito, y el canal 2 en la salida de R1.
Gráfica de la señal de entrada
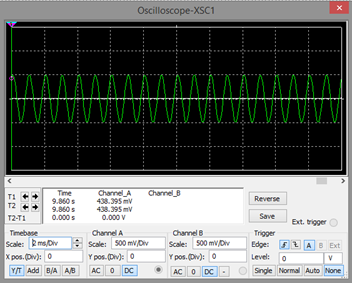
Gráfica de la señal de salida
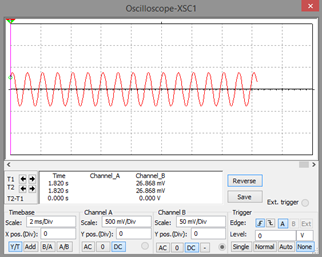
50mV/div 2ms/Div
Gráfica de la señal de entrada y salida
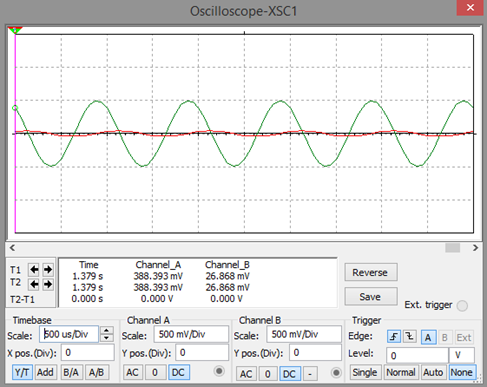
El filtro pasa bajo tiene la función de evitar que, en este caso, las frecuencias que están por encima de 79.5 Hz sean atenuadas. 1KHz es un valor que está muy por encima de la frecuencia de corte (79.5Hz), por ello la señal de salida tiene un valor alrededor de 50mVp.
- calcular la Fc para los siguientes casos (C=2uF) R1 = 10k Ohm, R2= 1K Ohm, R3= 100 Ohm
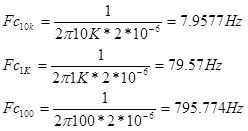
- Con el osciloscopio hallar la ganancia
Para una resistencia de 10K Ohms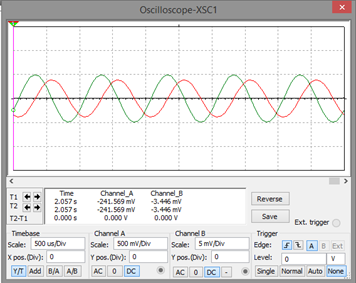
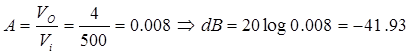
Para una resistencia de 1KOhms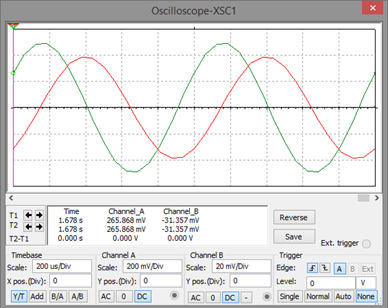
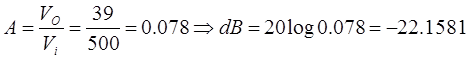
Para una resistencia de 100 Ohms
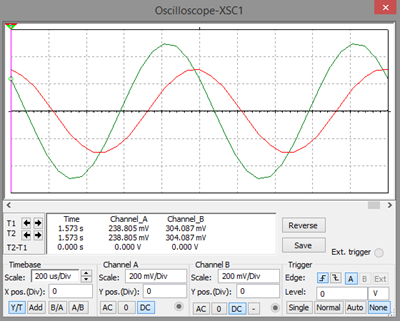
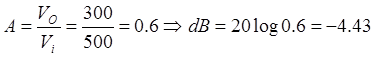
- Comparar el valor de la ganancia de tensión medido, con el valor ideal teórico.
Hallando los valores ideales
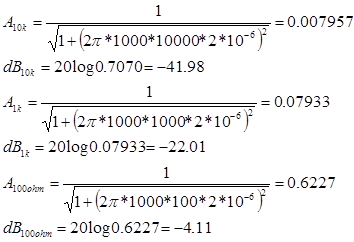
Valores teóricos
Resistencia Frecuencia de corte (Hz) Ganancia Av Ganancia dB 10K 7.9577 0.007957 -41.98 1K 79.577 0.07933 -22.01 100 795.77 0.6227 -4.11 Valores reales
Resistencia Frecuencia de corte (Hz) Ganancia Av Ganancia dB 10K 7.9577 0.008 -41.93 1K 79.577 0.078 -22.15 100 795.77 0.6 -4.43 - Realizar las gráficas del osciloscopio, variando la freciencia de entrada
Para una frecuencia de 10Hz, R= 1k Ohm y C= 2uF
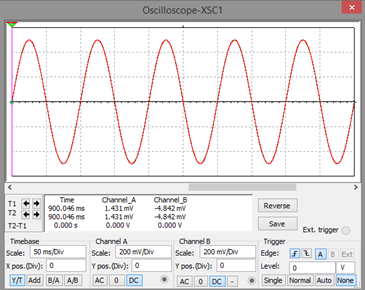
Ya que 10Hz está muy por debajo de la frecuencia de corte (79.5 Hz), el filtro no hará ninguna atenuación: las señales de salida y de entrada son iguales.
Para una frecuencia de 100 Hz
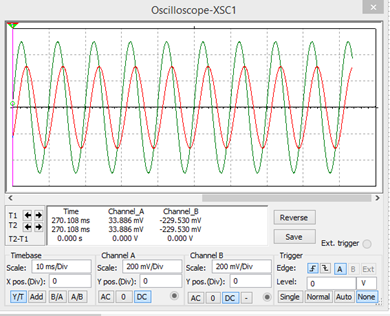
En este caso, cuando la frecuencia es mayor que la frecuencia de corte, se nota la atenuación.
Para una frecuencia de 1KHz
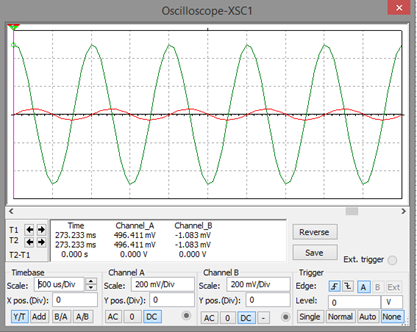
-
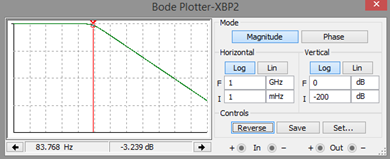
Realice los gráficos correspondientes de la respuesta en frecuencia (usando el Bode Plotter de Multisim)
Debido a que no se cambia ninguno de los componentes pasivos, la gráfica de bode no cambiará.
Filtro pasa altos
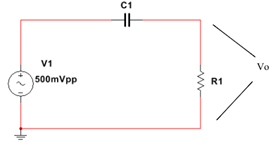
- Escribir las ecuaciones que definen las características siguientes:
Fc: frecuencia de corte
Av: Ganancia de tensión
G dB: Ganancia en decibeles
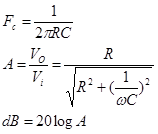
- Con los datos proporcionados calcular cada una de las características citadas:
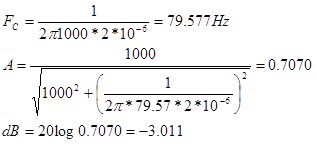
- Montar el circuito. Ajustar el generador de funciones para que proporcione una onda sonoidal de 500mV (pico) y frecuencia de 1KHz, y aplicar esta señal a la entrada del circuito. Finalmente, conectar a la entrada 1 del osciloscopio a la entrada del circuito, y el canal 2 en la salida de R1.
Gráfica de la señal de entrada
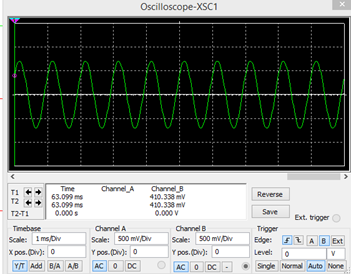
Gráfica de la señal de salida
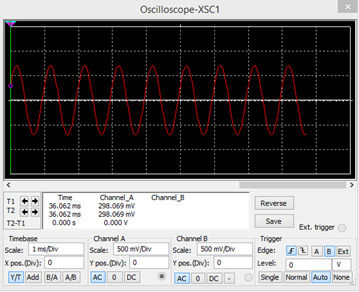
Las 2 gráficas en una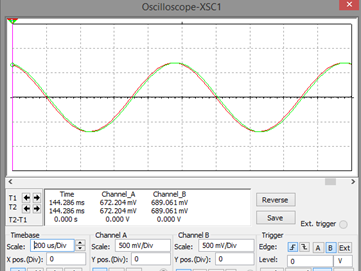
- Calcular la Fc para los siguientes casos (C= 2uF) R1= 10K Ohm, R2 = 1K Ohm y R3 = 100 Ohm
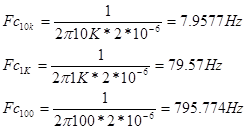
- Con el osciloscopio hallar la ganancia
Para una resistencia de 10K Ohms
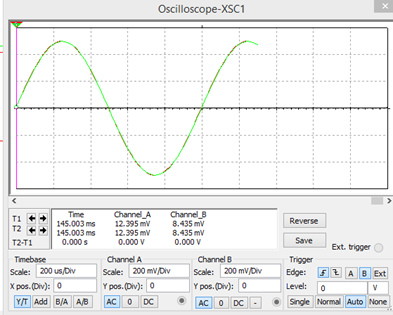
En la figura anterior se observa que la señal de entrada es exactamente igual a la señal de salida; por ello, se concluye que la ganancia es 1.
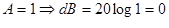
Para una resistencia de 1K Ohms
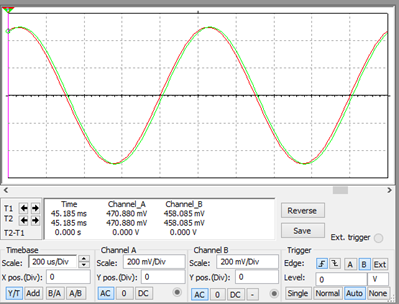
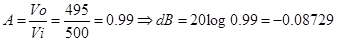
Para una resistencia de 100 Ohms
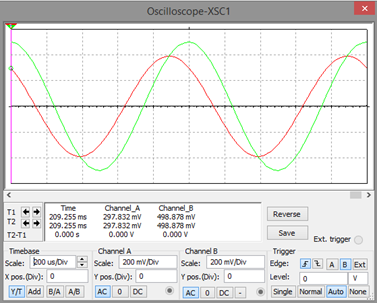
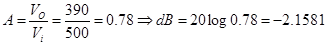
- Comparar el valor de la ganancia de tensión medido, con el valor ideal teóricos.
Hallando los valores ideales
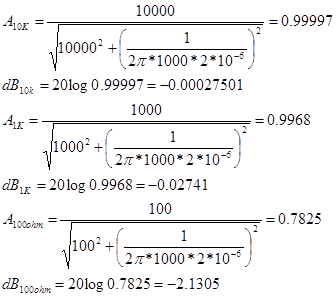
Valores teóricos
Resistencia Frecuencia de corte (Hz) Ganancia Av Ganancia dB 10K 7.9577 0.999997 -0.00027501 1K 79.577 0.9968 -0.02741 100 795.77 0.7825 -2.1305 Valores reales
Resistencia Frecuencia de corte (Hz) Ganancia Av Ganancia dB 10K 7.95577 1 -0.0027501 1K 79.577 0.99 -0.08729 100 795.77 0.78 -2.1581 - Realizar las gráficas del osciloscopio, variando la frecuencia de entrada.
Para una frecuencia de 10H<, R=1K Ohms y C= 2uF
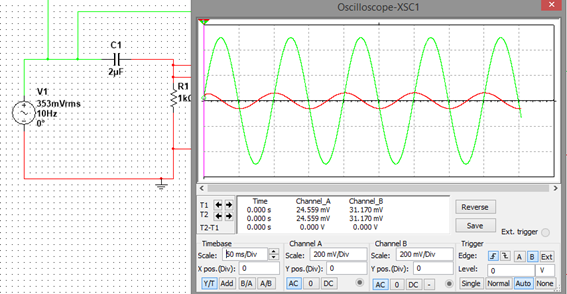
Para una frecuencia de 75 Hz
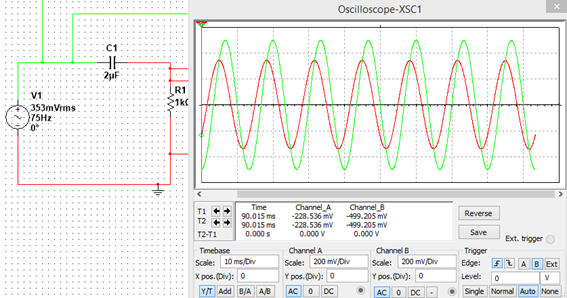
Para una frecuencia 500Hz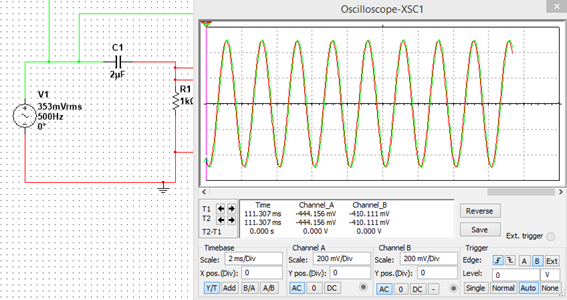
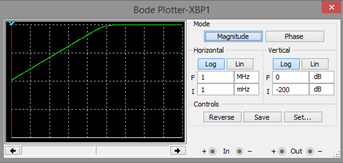
- Realice los gráficos correspondientes de la respuesta en frecuencia (usando el Bode Plotter de Multisim)
Debido a que no se cambia ninguno de los componentes pasivos, la gráfica de bode no cambiará.
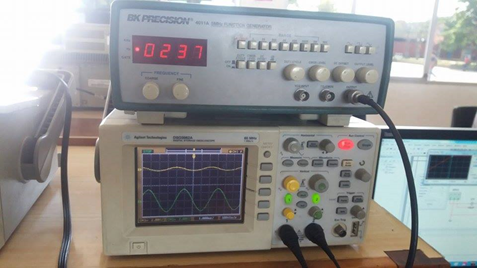
En el laboratorio

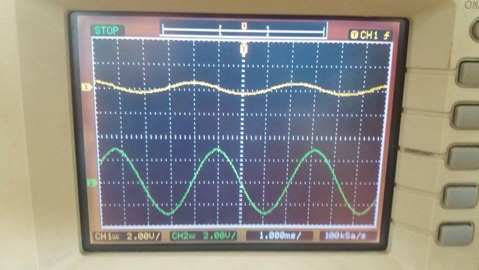
En este caso, la ganancia, será el siguiente:
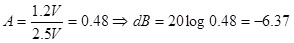
En el laboratorio, cuando se configuro el generador a una frecuencia baja (232 Hz), el filtro pasa alto atenúo esta señal.
Filtro Pasa Banda
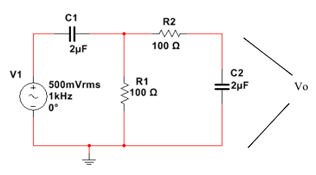
- Escribir las ecuaciones que definen las características siguiente:
Fc: frecuencia de corte
Av: Ganancia de tensión
G dB: Ganancia en decibeles
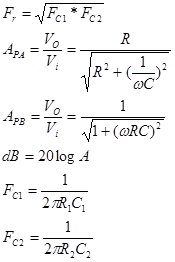
- Con los datos proporcionados calcular cada una de las características citadas
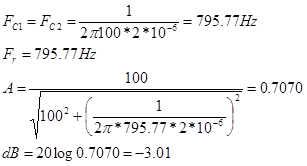
- Montar el circuito. Ajustar el generador de funciones para que proporcione una onda sonoidal de 500mV (pico) y frecuencia de 1KHz, y aplicar esta señal a la entrada del circuito. Finalmente, conectar a la entrada 1 del osciloscopio a la entrada del circuito, y el canal 2 en la salida de R1.
Gráfica de la señal de entrada
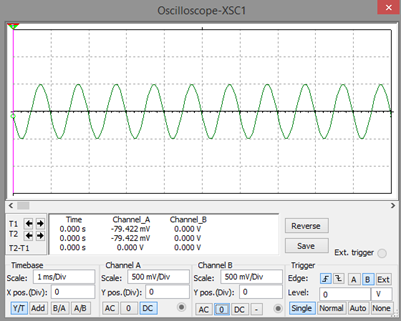
Gráfica de la señal de salida
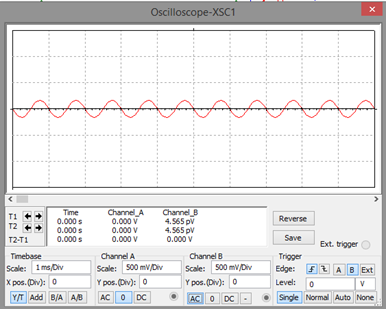
La señal de salida está atenuada al menos en un 50%
- En el osciloscopio medir las tensiones de entrada y salida, calculando a continuación la ganancia de tensión (Av).
De las dos últimas figuras anteriores, la ganancia será.
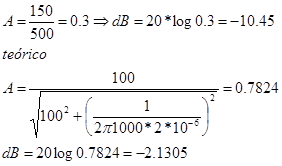
- Realizar las gráficas del osciloscopio, variando la frecuencia de entrada.
Para una frecuencia de 10 Hz
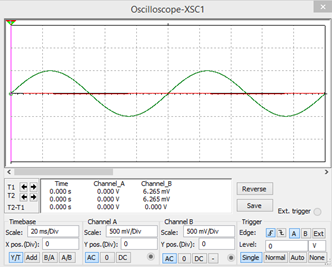
Como la frecuencia es menor que la frecuencia de corte, se da la atenuación de la señal de salida( color rojo).
Para una señal de 1KHz
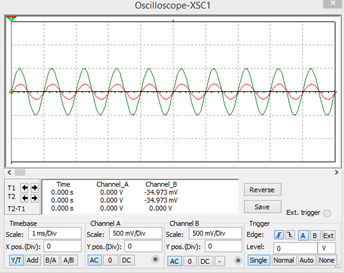
Los parámetros de los filtros pasivos, hacen que no se pueda llegar a una ganancia de 1
Para una señal de 20 KHz
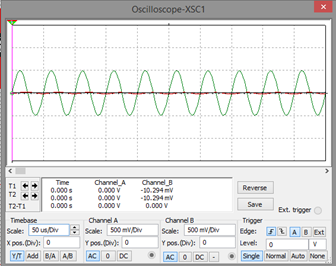
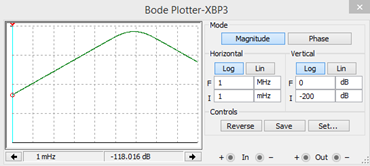
- Diagrama de bode
Si no se cambia los parámetros de los componentes pasivos, el diagrama de bode será solamente uno.
En el laboratorio

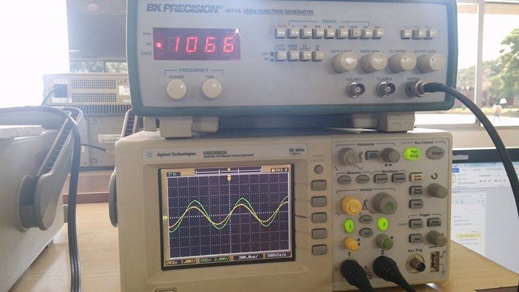
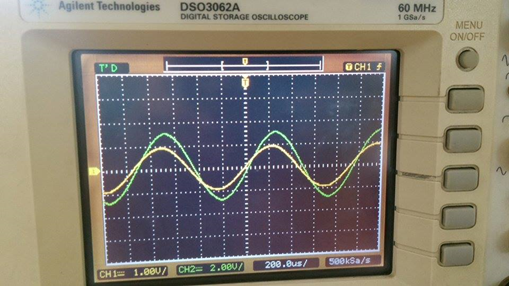
En este caso, la ganancia será.
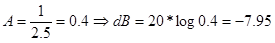
Filtro elimina banda
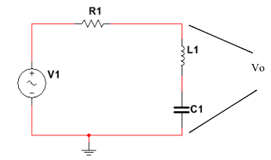
- Escribir las ecuaciones que definen las características siguientes:
Fc : frecuencias de corte
Av : Ganancia de tensión
G dB: Ganancia en decibeles
Fc1 y Fc2
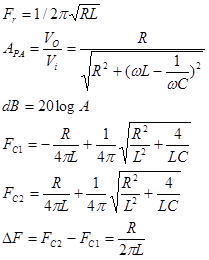
- Con los datos proporcionados calcular cada una de las características citadas
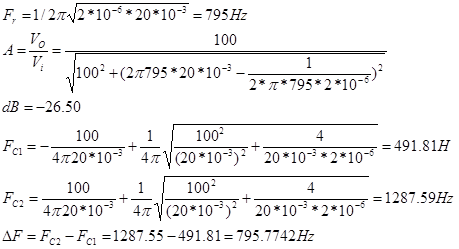
- Montar el circuito. Ajustar el generador de funciones para que proporcione una onda sonoidal de 500mV (pico) y frecuencia de 1KHz, y aplicar esta señal a la entrada del circuito. Finalmente, conectar a la entrada 1 del osciloscopio a la entrada del circuito, y el canal 2 en la salida de R1.
Gráfica de la señal de entrada
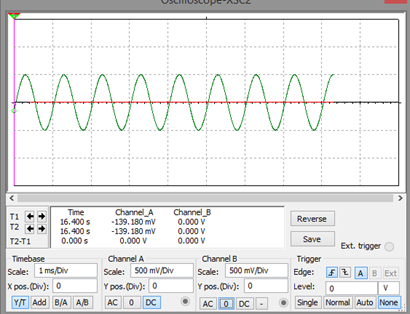
Gráfica de la señal de entrada
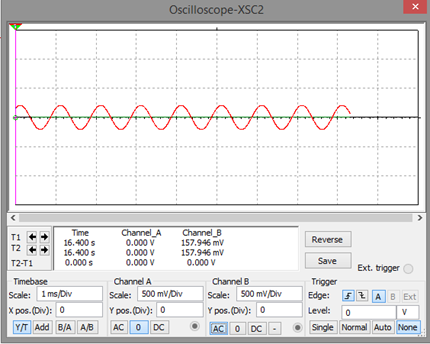
1KHz está en la zona de atenuación, ello se visualiza en la figura anterior.
- Calcular la ganancia
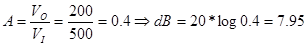
- Realizar las gráficas del osciloscopio, variando la frecuencia de entrada.
Para una frecuencia de 30 Hz
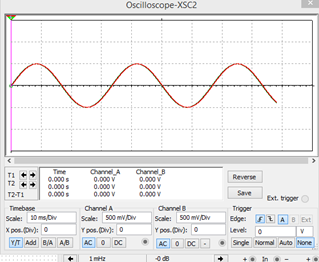
No se atenúa porque está fuera del ancho de banda.
Para una frecuencia de 800Hz
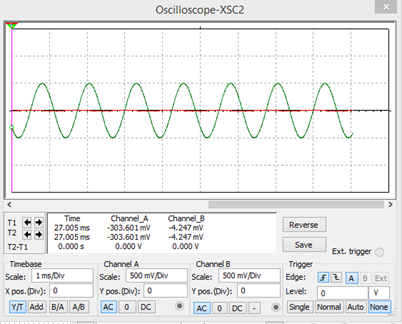
Si se atenúa porque 1KHz está dentro del ancho de banda
Para una frecuencia de 5KH<
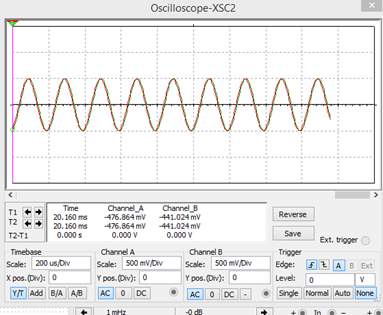
Está fuera del ancho de banda, por lo tanto no se atenúa.
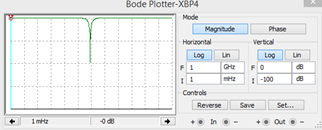
- Realice los gráficos correspondientes de la respuesta en frecuencia (usando el bode Plotter de Multisim)
Debido a que no se cambia ninguno de los componentes pasivos, la gráfica de bode no cambiará.
Conclusiones
- Los filtros ideales, en general, tienen un comportamiento que depende de su frecuencia de corte; sin embargo, en realidad, tienen un desfase que aumenta y disminuye a medida que se cambia la frecuencia.
- Los filtros pasa alto hacen que en su salida solo se muestren las frecuencias mayores a la de corte; las otras serán atenuadas o eliminadas.
- Los filtros pasa bajo hacen que en su salida solo se muestren las frecuencias menores a la Frecuencia de corte; las otras serán atenuadas o eliminadas.
- El filtro pasa banda cumple la función de dejar pasar frecuencias que estén en rango determinado por una frecuencia de corte 1 y 2, estas, a la vez, dependen de los parámetros de sus componentes pasivos.
- Los filtros elimina banda son capaces de eliminar frecuencias que están en un rango determinado por las frecuencias de corte 1 y 2, estas, a la vez, dependen del valor de sus componentes pasivos.
Aplicación de lo aprendido
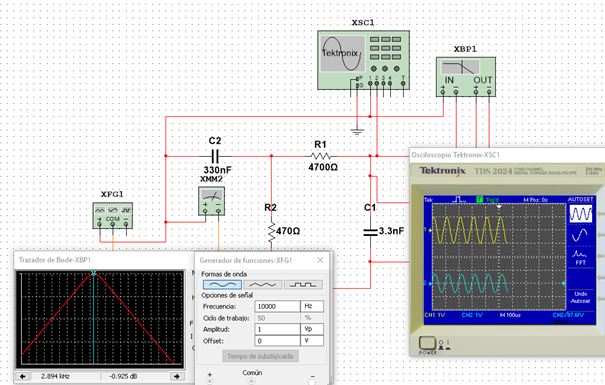
Diseñar un filtro pasivo pasa banda que presente una Fc1 de 1000 Hz y una Fc2 de 10 KHz
Ganancia de 0.702
El valor de R2 debe ser 10 veces menor. Se asumieron valores de capacitancia de 330nF y 3.3nF