Regresión exponencial

Objetivo

Determinar la función exponencial 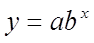de un conjunto de datos que tienen una tendencia exponencial.

Fundamento teórico

Sean los datos por tendencia exponencial

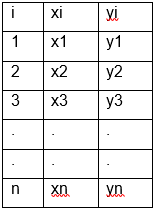
Calculo de a y b

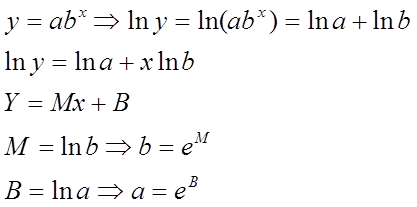
Calculo de M

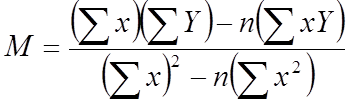
Calculo B

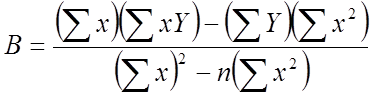
Procedimiento

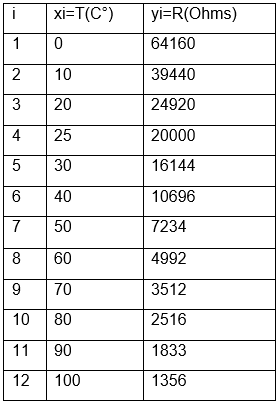
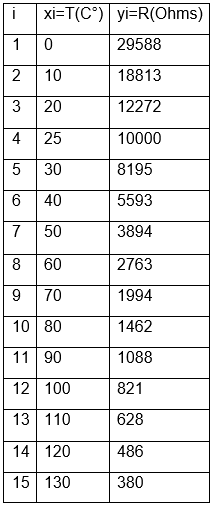
1. Se tiene los valores de temperatura y resistencia de un termistor NTC de 10k Ohms.

   

   Luego en Matlab se obtendrán las gráficas que representan la regresión exponencial de los datos del termistor. El código a continuación es el necesario:

   %regresión exponencial
   clc
   clear all
   close all
   %datos
   x=[0 10 20 25 30 40 50 60 70 80 90 100];
   y=[64160 39440 24920 20000 16144 10696 7234 4992 3512 2516 1833 1356];]
   nx=length(x);
   ny=length(y);
   %grafica de los datos
   figure(1)
   plot(x,y,'0')
   xlabel('Temperatura(C°)')
   ylabel('Resistencia(Ohms)')
   title('Termistor 20k')
   grid on
   %logaritmo de y
   yt=log(y);
   %calculo de M
   n=nx;
   sx=sum(x);
   sy=sum(yt);
   sxy=sum(x.*yt);
   sx2=sum(x.^2)
   M=(sx*sy-n*sxy)/sx^2-nsx2);
   %Calculo de B
   B=(sx*sxy-sy*sx2)/(sx^2-n*sx2);
   %Calculo de A
   a=exp(B);
   b=exp(M);
   ye=a*(b.^x);
   %grafica de la función exponencial
   figure(2)
   plot(x,y,'o',x,ye,'r')
   xlabel('Temperatura(C°)')
   ylabel('Resistencia( Ohms)')
   title('Termistor 20k')
   grid on
   disp(['el valor de a es:',num2str(a)]);
   disp(['el valor de b es:',num2str(b)]);
   

   El valor de a es: 54191.2582
   El valor de b es: 0.9624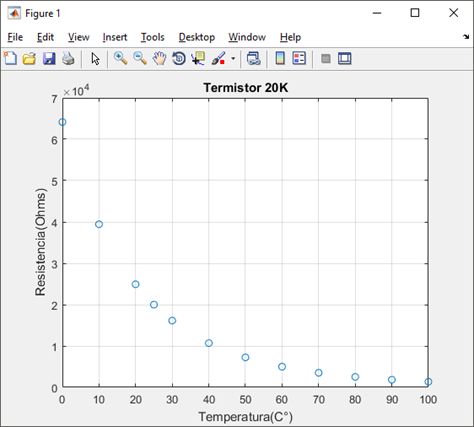

   

2. Realizar el mismo procedimiento para el termistor de 10k tipo 3 (0 a 130 C°)

   

   %regresión exponencial
   clc
   clear all
   close all
   %datos
   x=[0 10 20 25 30 40 50 60 70 80 90 100 110 120 130];
   y=[2958 18813 12272 10000 8195 5593 3894 2763 1994 1462 1088 821 628 486 380 ];
   nx=length(x);
   ny=length(y);
   %grafica de los datos
   figure(1)
   plot(x,y,'0')
   xlabel('Temperatura(C°)')
   ylabel('Resistencia(Ohms)')
   title('Termistor 10k')
   grid on
   %logaritmo de y
   yt=log(y);
   %calculo de M
   n=nx;
   sx=sum(x);
   sy=sum(yt);
   sxy=sum(x.*yt);
   sx2=sum(x.^2)
   M=(sx*sy-n*sxy)/sx^2-nsx2);
   %Calculo de B
   B=(sx*sxy-sy*sx2)/(sx^2-n*sx2);
   %Calculo de A
   a=exp(B);
   b=exp(M);
   ye=a*(b.^x);
   %grafica de la función exponencial
   figure(2)
   plot(x,y,'o',x,ye,'r')
   xlabel('Temperatura(C°)')
   ylabel('Resistencia( Ohms)')
   title('Termistor 10k')
   grid on
   disp(['el valor de a es:',num2str(a)]);
   disp(['el valor de b es:',num2str(b)]);
   

   El valor de a es: 13767.3248
   El valor de b es: 0.97309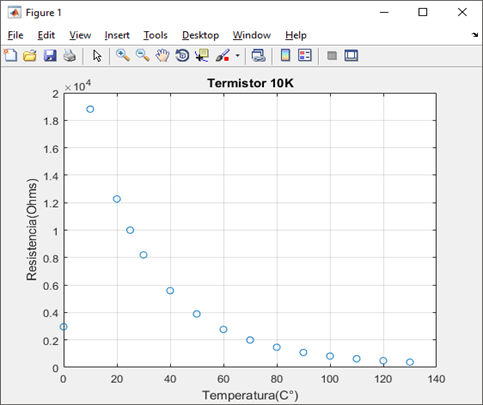

   

Conclusiones

Por lo antes mostrado es visible que Matlab es un software que vuelve practico el cálculo y la muestra grafica de una regresión exponencial.