Intemerdio > Matematica aplicada > valor eficaz, medio, derivación e integración de señales

Valor eficaz, medio, derivación e integración de señales

Objetivo

Utilizar las funciones de MatLab para obtener el valor eficaz y medio de una señal periodica

Fundamento teórico

Software MatLab

Es una herramienta de software matemático que ofrece un entorno de desarrollo integrado (IDE) con un lenguaje de programación propio (lenguaje M).

Entre sus prestaciones básicas se hallan: la manipulación de matrices, la representación de datos y funciones, la implementación de algoritmos, la creación de interfaces de usuario y la comunicación con programas en otros lenguajes y con otros dispositivos hardware. El paquete MATLAB dispone de dos herramientas adicionales que expanden sus prestaciones, a saber, Simulink (plataforma de simulación multidominio) y GUIDE (editor de interfaces de usuario - GUI). Además, se pueden ampliar las capacidades de MATLAB con las cajas de herramientas (toolboxes); y las de Simulink con los paquetes de bloques.

Es un software muy usado en universidades y centros de investigación y desarrollo. En los últimos años ha aumentado el número de prestaciones, como la de programar directamente procesadores digitales de señal o crear código VHDL.


Valor medio

Se llama valor medio de una tensión (o corriente) alterna a la media aritmética de todos los valores instantáneos de tensión (o corriente), medidos en un cierto intervalo de tiempo.

En una corriente alterna sinusoidal, el valor medio durante un período es nulo: en efecto, los valores positivos se compensan con los negativos. Vm = 0


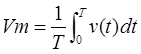
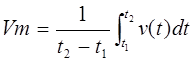
Periodo de la señal


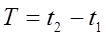
Valor eficaz

Se define el valor eficaz de una corriente alterna, como aquel valor que llevado a corriente continua nos produce los mismos efectos caloríficos. Es un valor característico, que por otra parte es el que proporcionan los instrumentos de medida, ya sean analógicos o digitales. Aunque en la actualidad ya existen instrumentos digitales que proporcionan otros parámetros de la señal alterna.



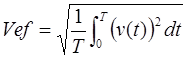
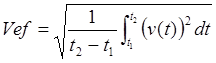
Periodo de la señal:


Desarrollo

  1. Derivador
    Código de MatLab:
    • %Derivada de una función
    • clc
    • close all
    • clear all
    • %Declaración de la variable independiente
    • syms t
    • %funciones
    • f1=t*exp(t^2);
    • f2=cos(4*t)*sin(10*t);
    • f3=(t+2)*cos(t^2);
    • f4=(2*t^2-4)*exp(8*t);
    • f5=(5*t^3-6)*sin(2*t);
    • %Derivadas
    • f1d=diff(f1);
    • f2d=diff(f2);
    • f3d=diff(f3);
    • f4d=diff(f4);
    • f5d=diff(f5);

    Resultados

    • f1= t*exp(t^2)
    • f1d= exp(t^2)+2*t^2*exp(t^2)
    • f2= cos(4*t)*sin(10*t)
    • f2d= 10*cos(4*t)*cos(10*t)-4*sin(4*t)*sin(10*t)
    • f3= cos(t^2)*(t+2)
    • f3d= cos(t^2)-2*t*sin(t^2)*(t+2)
    • f4=exp(8*t)*(2*t^2-4)
    • f4d= 4*t*exp(8*t)+8*exp(8*t)*(2*t^2-4)
    • f5= sin(2*t)*(5*t^3-6)
    • f5d= 2*cos(2*t)*(5*t^3-6)+15*t^2*sin(2*t)
  2. Aplicación de la integral

    Código de MatLab:

    • %Aplicaciones de la integral
    • clc
    • close all
    • clear all
    • %Declaración de la variable independiente
    • syms t
    • %funciones
    • f1=t^4;
    • f2=sin(9*t);
    • f3=t*log(8*t);
    • f4=exp(2*t)*sin(4*t);
    • f5=sin(3*t)*cos(4*t);
    • %integrales indefinidas
    • f1i=int(f1);
    • f2i=int(f2);
    • f3i=int(f3);
    • f4i=int(f4);
    • f5i=int(f5);
    • %integral definida
    • f1id=int(f1,0,2);
    • f2id=int(f2,0,pi);
    • f3id=int(f3,1,3);
    • f4id=int(f4,0,1);
    • f5id=int(f5,0.5,1);

    Resultados:

    • f1=t^4
    • f1i=t^5/5+c
    • f1id=32/5
    • f2=sin(9*t)
    • f2i=-cos(9*t)/9+c
    • f2id=2/9
    • f3=t*log(8*t)
    • f3i=(t^2*(log(8*t)-1/2))/2+c
    • f3id=log(331776*3^(1/2))-2 =11.2615
    • f4=exp(2*t)*sin(4*t)
    • f4i=-(exp(2*t)*(4*cos(4*t)-2*sin(4*t)))/20+c
    • f4id=1/5 - (exp(2)*(2*cos(4) - sin(4)))/10 = 0.6068
    • f5=sin(3*t)*cos(4*t)
    • f5i=cos(t)/2 - cos(7*t)/14+c
    • f5id=cos(1)/2 - cos(1/2)/2 - cos(7)/14 + cos(7/2)/14 = -0.2894


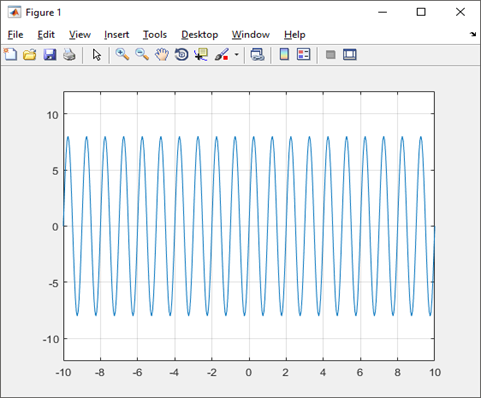
  3. Valor medio y eficaz de una función senoidal

    Gráfica de la señal senoidal


    Código para MatLab

    • %valor medio y eficaz de una señal senoidal
    • clc
    • clear all
    • close all
    • syms A T t
    • f=1/T;
    • ft=A*sin(2*pi*f*t);
    • %valor medio
    • vm=(1/T)*int(ft,0,T);
    • %valor eficaz
    • vef=((1/T)*int(ft^2,0,T))^0.5;

    Resultado:

    • ft=A*sin(2*pi*f*t)
    • vm= 0
    • vef=(A^2/2)^(1/2)= A/(2^0.5)
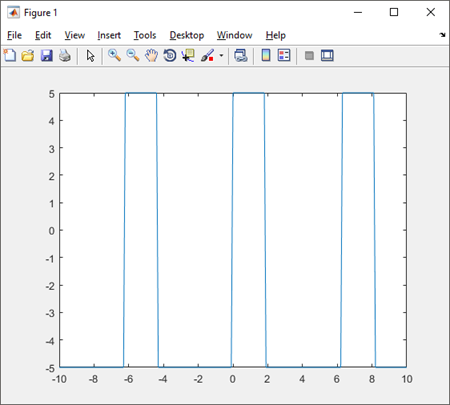
  4. Valor medio y eficaz de una función cuadrada

    Gráfica de la señal cuadrada



    Código para MatLab:

    • %valor medio y eficaz de una señal cuadrada
    • clc
    • clear all
    • close all
    • syms A T t
    • %intervalo de integración
    • d=[0 T/2 T];
    • %función cuadrada
    • f=[A -A];
    • f= sym(f);
    • %valor medio inicial
    • vm0=0;
    • for i=1 : length (f)
    • vm0=vm0+int(f(i),'t',d(i),d(i+1));
    • end
    • %valor medio final
    • vm=(1/T)*vm0;
    • %valor eficaz inicial
    • vef0=0;
    • for i=1:length(f)
    • vef0=vef0+int (f(i)^2,'t',d(i),d(i+1));
    • end
    • %valor eficaz final
    • vef=((1/T)*ve0)^0.5;

    Resultados

    • f= [A -A]
    • vm= 0
    • vef= (A^2)^(1/2)
  5. Valor medio y eficaz de una onda triangular

    Gráfica de la señal triangular continua


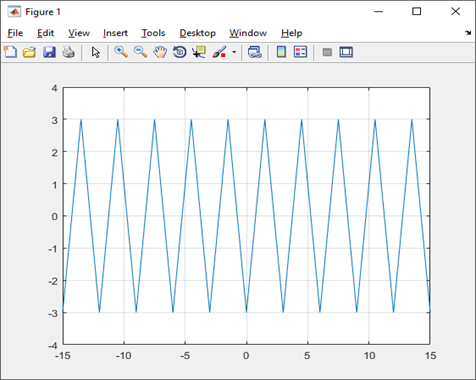
    Código para MatLab

    • %Valor medio y eficaz de una señal triangular
    • clc
    • clear all
    • close all
    • syms A t
    • T=10;
    • f=1/T;
    • ft=A*sawtooth(2*pi*0.1*f,0.5);
    • %valor medio
    • vm=(1/T)*int(ft,0,T);
    • %valor eficaz
    • vef=((1/T)*int(ft^2,0,T))^0.5;

    Resultados:

    ft= A/sawtooth(2*pi*0.1*f,0.5)

    vm = -24/5

    vef= 768^(1/2)/5 = 5.5426

  6. Valor medio y eficaz de una señal Dirichlet

    Gráfica de la señal Dirichlet


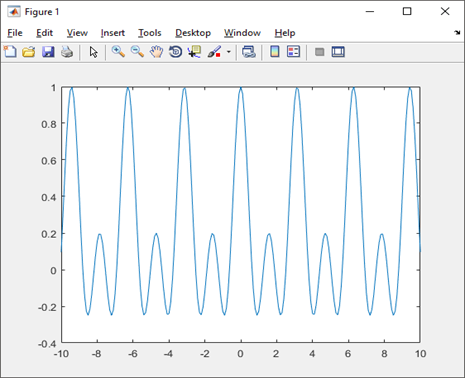
    Código para MatLab

    • %Valor medio y eficaz de una señal Dirichlet
    • clc
    • clear all
    • close all
    • syms A t
    • T=10;
    • f=1/T;
    • ft=A*diric(2*f,5);
    • %valor medio
    • vm=(1/T)*int(ft,0,T);
    • %valor eficaz
    • vef=((1/T)*int(ft^2,0,T))^0.5;

    Resultados:

    ft=A*diric(2*pi,5)

    vm= 4.8023

    vef= 5.5452

  7. Valor medio y eficaz de la señal diente de sierra

    Gráfica de la señal diente de sierra (sawtooth)



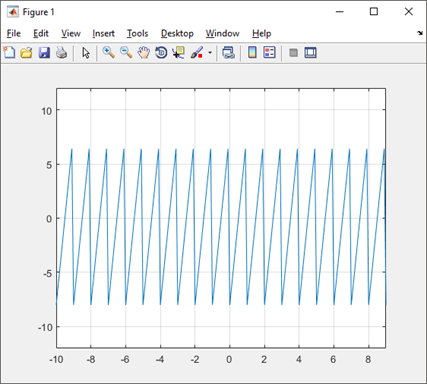
    Código para MatLab:

    • %Valor medio y eficaz de una señal diente de sierra
    • clc
    • clear all
    • close all
    • syms A t
    • T=10;
    • f=1/T;
    • ft=A*sawtooth(2*pi*f,1);
    • %valor medio
    • vm=(1/T)*int(ft,0,T);
    • %valor eficaz
    • vef=((1/T)*int(ft^2,0,T))^0.5;

    Resultado:

    ft= A*sawtooth(2*pi*f,1)

    vm = -4

    vef = (8*3^(1/2))/3 = 4.6188

Observaciones:

  • Al querer integrar o derivar una función no se puede graficar la señal.
  • Se debe tener en cuenta que en ciertas señales no son periódicas puesto se utiliza solo un periodo para determinar el valor medio.
  • En la gráfica de la señal triangular se utilizó el comando “sawtooth” dado que la función triangular continua es una forma especial de esta señal. Para graficarla se toma específicamente la frecuencia de 0.5 específicamente.
  • Para poder graficar las señales se debe remplazar la frecuencia (f) por la frecuencia (t), además de comentar la línea “syms” y darles valores a las variables. Como recomendación añadir el comando axis para centrar la señal en mitad de la gráfica.

Conclusiones:

  • Al conocer el funcionamiento de los comandos para generar funciones, se pueden modificar los parámetros para dar formas a las señales y de esta forma convertirlas en la señal deseada.
  • Poder generar estas funciones digitalmente es útil para simular algunos procesos y así estudiar los posibles fenómenos a estudiar.
  • Matlab es un entorno amigable para entender y aprender código de una manera fácil y rápida.
Linksappsclose
Fork me on GitHubcode Follow mokuzaru on Twittershare Visit mokuzaru Websitelink