Filtros activos
Introducción
Los filtros activos están compuestos de componentes pasivos, más amplificadores operacionales; estas cumplen una función muy importante en electrónica, la cual es filtrar las señales que no se desean en un proceso, y darle una ganancia determinada a la señal de salida.
Los filtros activos tienen grandes ventajas respecto a los pasivos, por ello son usados en la mayoria de casos.
En este laboratorio se aprenderá el principio de funcionamiento de estos, sus arreglos y los diferentes usos que tienen.
Objetivos
- Restringir las componentes de frecuencia de una señal dada.
- Analizar la respuesta en frecuencia de un filtro.
Equipos y materiales
- Osciloscopio
- Fuente de alimentación dual
- Generador de funciones
- Multímetro
- Protoboard
- (01) 15K 1/4w
- (01) 30K 1/4w
- (01) TL081
- (02) 0.001 uF
- Manual de reemplazos
- Cable de conexión
Marco teórico
Transformada de Laplace
La trasformada de Laplace es un tipo de transformada integral empleada con mucha frecuencia para el estudio de señales y sistemas de control. Básicamente la transformada de Laplace se define como:
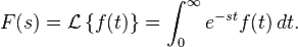
Laplace transforma nuestra ecuación que se encuentra en función a t, a una ecuación en función a S, haciendo así más fácil el análisis.
Función de transferencia
La función de transferencia se define como la transformada de Laplace de la señal de entrada sobre la transformada de Laplace de la señal de salida.

Trabaj en el dominio de Laplace no solamente es útil para la resolución matemática de ecuaciones, sino que se presta especialmente para ser utilizado con el concepto de función de transferencia. En general un proceso recibe una entrada u(t) y genera una salida y(t). Si llevamos estas señales al dominio de Laplace tendremos una entrada U(s) que genera una salida Y(s). La función que relaciona salida con entrada se denomina función de transferencia g(s).
Filtros activos
En los filtros activos, la separación de la señal ocurre mientras se amplifica la frecuencia. Es por supuesto un filtro activo, porque requiere de la energía eléctrica para funcionar y puede proporcionar, además de la atenuación y separación de las otras líneas, un incremento de nivel en caso de necesidad. Por el contrario, un filtro pasivo se coloca entre el amplificador y el altavoz y se convierte en parte integral de él tomando energía del amplificador para su operación. No se puede lograr una ganancia en las vías, en realidad, se introducen algunas atenuaciones.

Procedimiento
primera parte: Filtro pasa bajas
- Montar el circuito de la figura 1 y conectar a la fuente de alimentación.
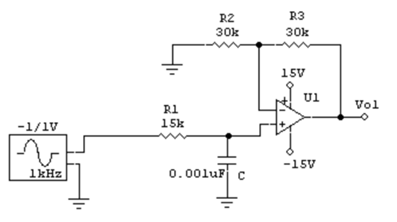

- Ajustar el generador de señal para tener una tensión senoidal de 1V (de pico) y 1KHz de frecuencia.

- Conectar el canal 1 del osciloscopio a la entrada del circuito y el 2 a la salida.
- Aplicar la señal senoidal al circuito. Mida con el osciloscopio la amplitud de la señal de salida y determine la ganancia del filtro.
Voltaje de entrada (verde) : 1V/div voltaje de salida (amarillo): 500mV/div Tiempo: 200us/div Teorico:
Vo1 = 2V Av = Vo1 / Vi = 2/1 = 2V Av(dB) = 10*log2 = 6.02 dB Experimental:
Vo1 = +/- 1V Av = 1.81 Av(dB) = 5.5154 dB -
Compare las señales de entrada y salida. ¿Existe alguna distorsión en la señal?
No se repara ninguna distorsión. -
Existe desfase entre las dos señales.
Teórico:
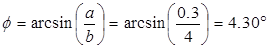
Experimental:
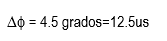
-
Varíe la frecuencia del generador incrementándolo hasta que la amplitud de la señal de salida disminuya a un valor igual al 70.7% del valor obtenido en el paso 4.
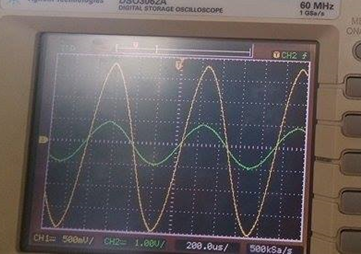
Voltaje de entrada(verde): 1V/div Voltaje de salida (amarillo):500mV/div Tiempo: 200us/div
A una frecuencia de 1000Hz se obtiene el voltaje máximo; por lo tanto:
Teórico:
Vmax = 2V ==> 70% Vmax = 0.7*2 = 1.4V
Experimental:
V salida (1KHz) = +/- 1.81 v
70.7% V salida (1KHz) = +/- 1.28 V
Ubicamos el valor de 1.4 V en la salida y, variando la frecuencia, hacemos que el voltaje pico de la salida coincida con este valor (1.4V).
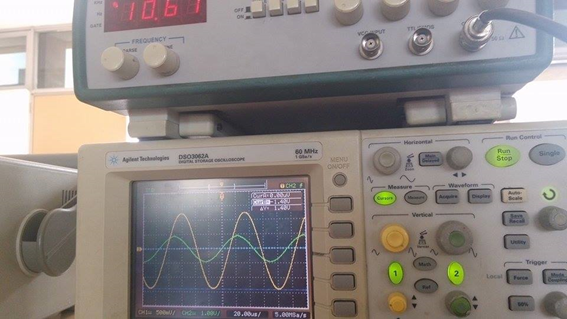
Voltaje de entrada(verde): 1V/div Voltaje de salida (amarillo):500mV/div Tiempo: 200us/div
La frecuencia de corte es cuando el voltaje está a un 70% del voltaje máximo:
Fc=10.61 KHz
Calcule teóricamente este valor mediante la expresion:
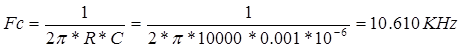
- ¿Las dos frecuencias de corte son iguales?
Las frecuencias de corte, halladas de forma teórica y práctica, son iguales. - Siga incrementando la frecuencia del generador hasta que la amplitud sea menor al 10% de la amplitud de la señal de salida a la frecuencia de 1KHz. En este instante mida la frecuencia.
Teórico (haciendo uso de multisim):
V 10% max = 0.1*2 = 0.2V
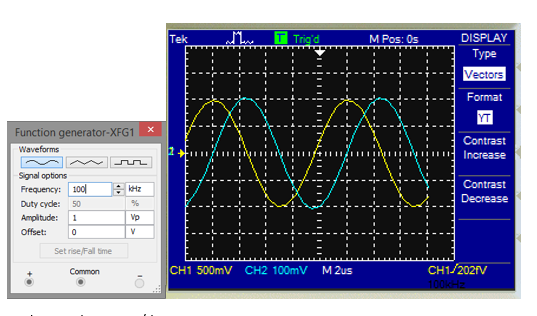
Voltaje de entrada: 500mV/div Voltaje de salida (azul):100mV/div La frecuencia para un voltaje de 0.2 V: F = 100 KHz
Experimental:
F = 85.16 KHz
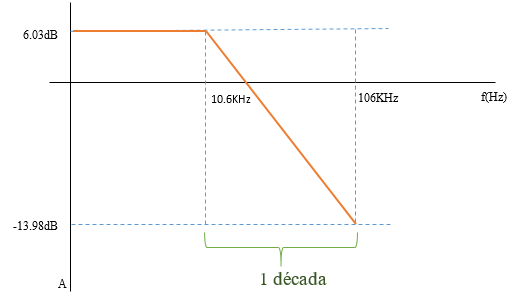
- Determine la pendiente de caída del filtro en dB/dec.
- A una frecuencia de 1000Hz obtenemos la ganancia máxima, que es 6.03 dB. Nuestro primer punto será (1000Hz, 6.03 dB)
- Hallamos la década:
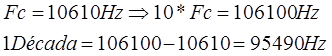
El voltaje pico para una frecuencia de 106100 Hz
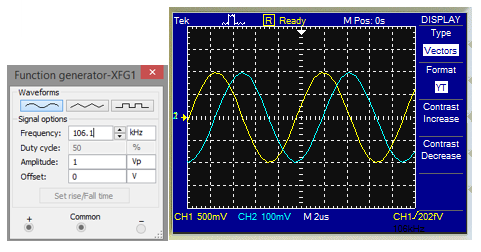
Voltaje de entrada (amarillo): 500mV/div Voltaje de salida (azul):100mV/div
v = 0.2 V
Av = 0.2 / 1 = 0.2
dB = 20*log0.2 = -13.97 dB
Teórico:
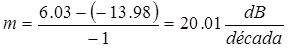
Experimental:
m = 18.062 dB/década
Segunda parte: Filtros pasa altos
- Montar el circuito de la Figura 2 y conectar la fuente de alimentación.

- Ajustar el generador de señal para tener una tensión senoidal de 1V (de pico) y 100KHz de frecuencia.
En nuestro caso hemos utilizado 54.14 KHz

- Conectar el canal 1 del osciloscopio a la entrada del circuito y el 2 a la salida
Voltaje de entrada (verde): 500mV/div Voltaje de salida (amarillo):500mV/div Tiempo : 5 us/div
- Aplicar la señal senoidal al circuito. misa con el osciloscopio la amplitud de la señal de salida y determine la ganancia del filtro.
Teórico:
Vo1 =2V
Av = Vo1/Vi = 2/1 = 2V
Av(dB) = 20*log2= 6.02dB
Experimental:
Vo2 = +/-1.81 V
Av = 1.8
Av(dB) = 5.15 dB
- ¿Compare las señales de entrada y de salida. Existe alguna distorsión en la señal?
Sí existe distorsión en la señal. - Existe desfase entre las señales. Anote el valor.
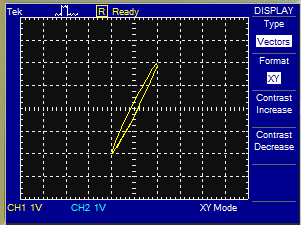
Teórico:
Experimental:

- Varíe la frecuencia del generador decrementándolo hasta que la ampitud de la señal de salida disminuya a un valor igual al 70.7% del valor obtenido en el paso 4.
El valor máximo del voltaje es 2V, por lo tanto su 70% será.
Vmax = 2V
V70% = 0.7*2 = 1.4V
¿A qué frecuencia se obtiene este valor de amplitud?

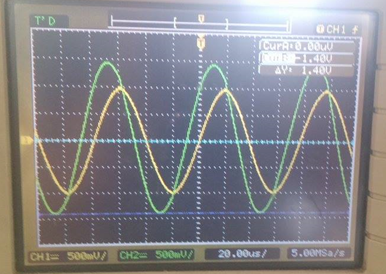
Voltaje de entrada (verde): 500mV/div Voltaje de salida (amarillo):500mV/div Tiempo : 20 us/div
Fcorte = 12.87 KHz
Teóricamente:
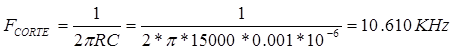
- ¿Las dos frecuencias de corte son iguales?
Tiene una diferencia de 2.2 KHz, lo cual se debe a un error en la medición.
- Siga decrementando el valor de la frecuencia del generador hasta que la amplitud sea menor al 10% de la amplitud da la señal de salida a la frecuencia de 100 KHz. En este instante mida la frecuencia.
Teórico:
Vmax = 2V ==> V10% = 0.1*2 = 0.2V
A = 0.2/1 = 0.2
dB = 10*log 0.2 = -13.97dB
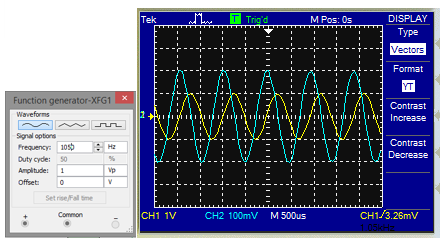
Voltaje de entrada (azul): 100mV/div Voltaje de salida (amarillo):1V/div Tiempo : 500 us/div
Por lo tanto:
F10% = 1050 Hz
Experimental
f = 1.2KHz
- Determinar la pendiente de caída del filtro en dB/dec
Teórico:
Como Fc = 10.6 KHz
para una decada:
Fdecada = 10.6 /10 = 1.06 KHz
La señal para 1.06 KHz
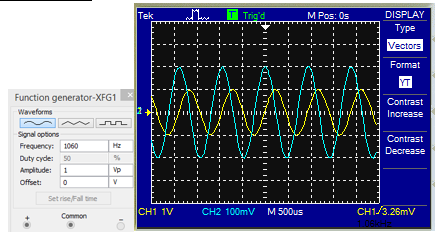
Voltaje de salida (azul): 100mV/div Voltaje de entrada (amarillo):1V/div Tiempo : 500 us/div
Entonces, la ganancia:
A = 0.2/1 = 0.2
dB = 20*log0.2 = -13.98
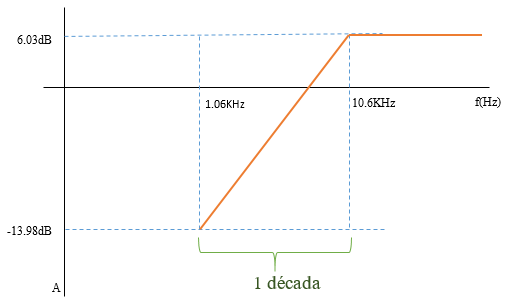
Finalmente:
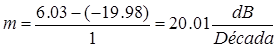
Experimental:
m = 18.05 dB/dec
Tercera parte: Filtro pasa banda
- Montar el circuito de la Figura 3 y conectar la fuente de alimentación
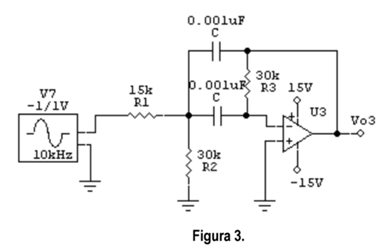
- Ajustar el generador de señal para tener una tensión senoidal de 1V (de pico) y 10KHz de frecuencia.
-
conectar el canal 1 del osciloscopio a la entrada del circuito y el 2 a la salida.
-
Aplicar la señal senoidal al circuito. Ajuste la frecuencia del generador hasta sintonizar la máxima amplitud de salida. Mida y anote la frecuencia y la amplitud, determine la ganancia del filtro.
Voltaje de entrada (verde): 500mV/div Voltaje de salida (amarillo): 500mV/div Tiempo : 50 us/div
Fcentral = 10.20 KHz
Vo3 = 0.95V
Av = 0.95/1 = 0.95
dB = 10log0.95 = -0.4455dB
- Compare las señales de entrada y salida.¿Existe alguna distorsión en la señal?
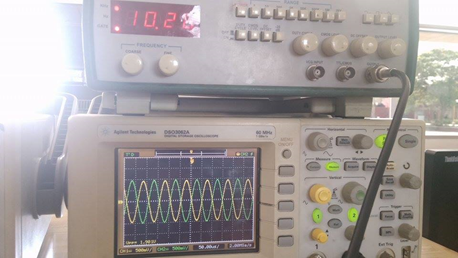
No existe ninguna distorsión en las señales. - Existe desfase entre las señales. Anote el valor.
- Varíe la frecuencia del generador
- Primero incrementándola hasta que la amplitud de la señal de salida disminuya a un valor igual al 70.7% del valor obtenido en el paso 4.
Vsalida = 0.95 V
V70% = 0.95/0.7 = 0.67V
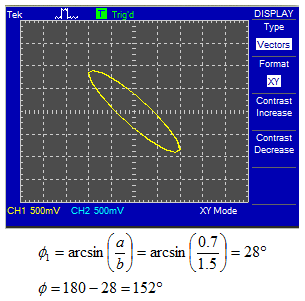
Voltaje de entrada (verde): 500mV/div Voltaje de salida (amarillo): 500mV/div Tiempo : 20 us/div
¿A qué frecuencia se obtiene este valor de amplitud?
Fcortes_superior = 14.15 KHz
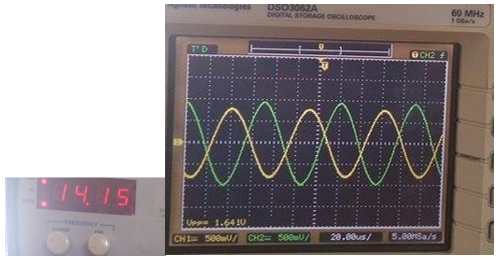
- Ahora decremente la frecuenia hasta que la amplitud de la señal de salida disminuya a un valor igual al 70.7% del valor obtenido en el paso 4.
Vsalida = 0.95V
V70% = 0.95*0.7 = 0.67V

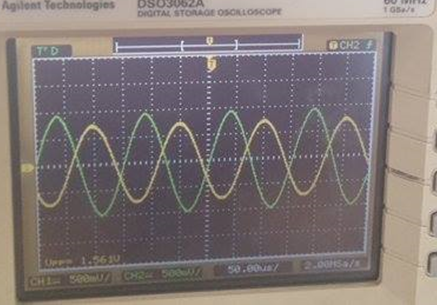
Voltaje de entrada (verde): 500mV/div Voltaje de salida (amarillo): 500mV/div Tiempo : 50 us/div
¿A qué frecuencia se obtiene este valor de amplitud?
Fcorte_inferior = 6.58 KHz
Entonces:
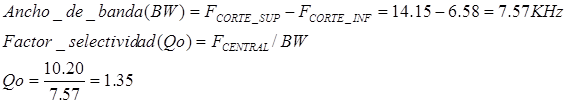
Un filtro con menor ancho de banda (mayor Q), será mejor que otro con más ancho de banda.
Cálculo de la frecuencia teórica
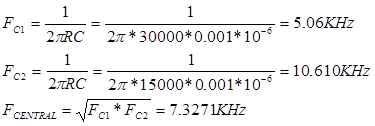
- Primero incrementándola hasta que la amplitud de la señal de salida disminuya a un valor igual al 70.7% del valor obtenido en el paso 4.
-
¿La frecuencia central teórica y media son iguales?
La frecuencia central teórica y práctica difieren, alrededor de 3kHz; se debe a que hay una banda donde la ganancia es similar, lo cual hace que la visualización, en el osciloscopio, de la frecuencia central, no sea idónea.
-
Ahora usando el mismo método usado para el filtro pasa altos y pasa bajos determine el valor de la pendiente de caída superior e inferior en dB/dec.
Década para el filtro pasa alto y pasa bajo.
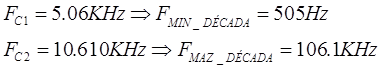
Para una frecuencia de 505 HZ.
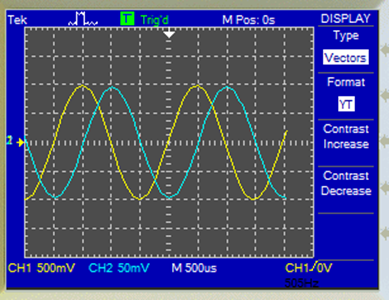
Voltaje de entrada (amarillo): 500mV/div Voltaje de salida (azul): 500mV/div Tiempo : 500 us/div
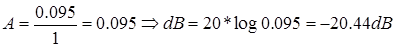
Para una frecuencia de 106.1 KHz
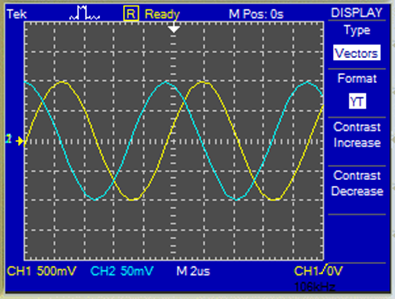
Voltaje de entrada (amarillo): 500mV/div Voltaje de salida (azul): 50mV/div Tiempo : 500 us/div
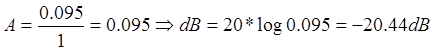
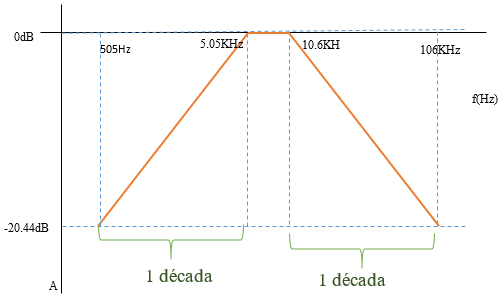
Entonces:
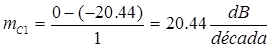
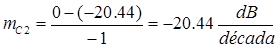
Conclusiones
- En un filtro de primer orden, la pendiente, en una década, siempre tendrá un valor cercano a +-20dB/dec, que es la pendiente ideal.
- Los filtros activos tienen un comportamiento similar a los filtros pasivos, la única diferencia es que, gracias al amplificador operacional, el resultado puede ser amplificado, lo cual depende del arreglo del amplificador.
- La amplificación de un filtro activo tiene un tope, la cual es la alimentación del amplificador operacional.
- Debido a las características del amplificador operacional, un filtro activo, no puede trabajar a frecuencias muy elevadas.
- Los filtros activos pasa bajo dejan pasar frecuencias menores a la frecuencia de corte, y, dependiendo del arreglo en el amplificador operacional, aumentan a la salida una ganancia determinada.
- Los filtros pasa alto dejan pasar frecuencias mayores a la frecuencia de corte, y, dependiendo del arreglo en el amplificador operacional, aumentan a la salida, una ganancia determinada.
- Los filtros pasa banda dejan pasar frecuencias que estén en dentro del ancho de banda (WB), y, dependiendo de la configuración del amplificador operacional, aumentarle o disminuirle una ganancia determinada.
Observaciones
- Lo idóneo sería hacer primero la teoría, antes de laboratorio.
aplicación de lo aprencido
diseñar un filtro pasa banda
- De cuarto orden
- Ganancia de 5
- Frecuencia central 1KHz
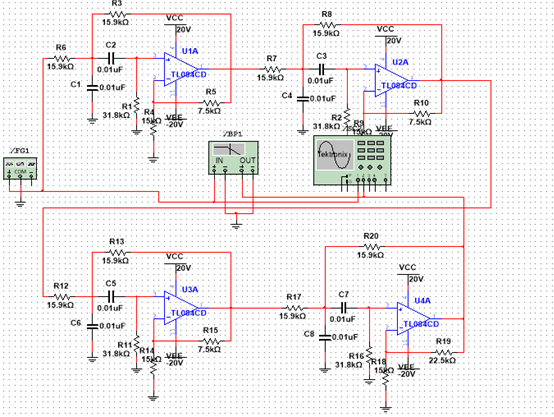
Para el diseño de este filtro pasa banda de cuarto orden se realizará un arreglo de cuatro filtros pasa banda tipo Sallen-Key, que son empleados para anchos de banda estrechos. Ya que usando un arreglo con filtros pasa banda convencionales se conseguía una frecuencia de resonancia demasiado atenuada, se optó por emplear el filtro Sallen-Key.
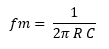
Para lo cual se define C= 0.01 uF, y se calcula R para una frecuencia de resonancia igual a 1 Khz.
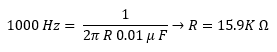
Se conectan los cuatro filtros de primer orden en serie, consiguiendo así un filtro de cuarto orden, 80db/década.
La ganancia en cada filtro está determinada por la relación de las resistencias conectadas a la entrada inversora del OPAMP.
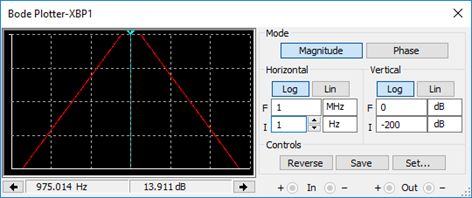
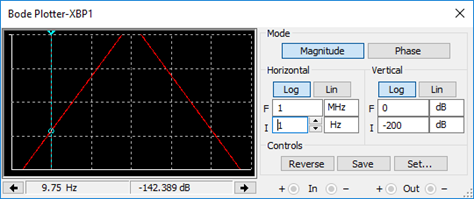
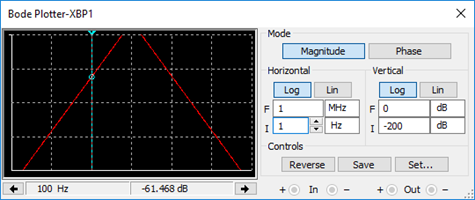
En el diagrama mostrado se expresa el comportamiento de la señal en función al valor de frecuencia que tenga esta. También se evidencia que el filtro es de cuarto orden, siendo que la variación de la atenuación es de 80db por década.
Ganancia de 5
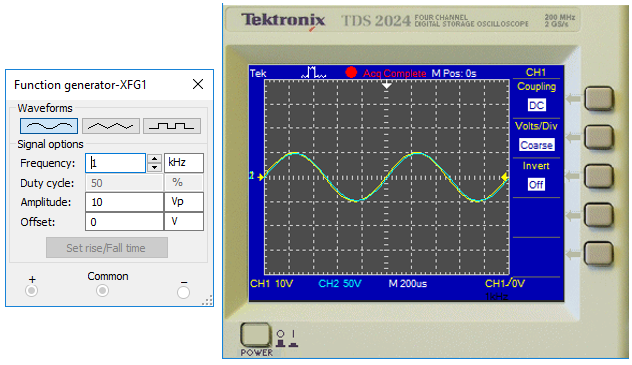
Comportamiento de las señales entrada y salida a una frecuencia de 1KHz, frecuencia de resonancia. Presenta una ganancia de 5.
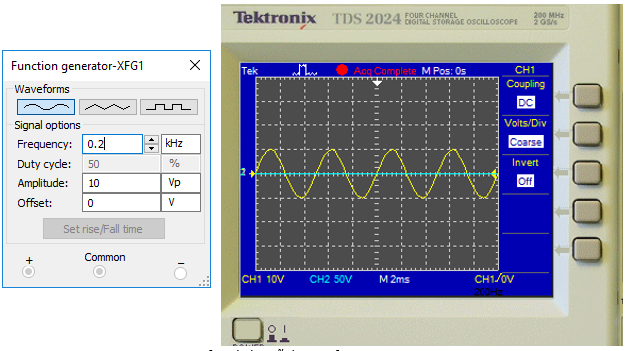
En la gráfica se muestran las señales de entrada (amarilla) y salida (turquesa) a una frecuencia de 200 Hz, se observa la señal de salida es atenuada y casi es igual a 0V.
